【EEA】量化玩家对单因素的期望胜率

题目

本文是笔者在探娱研究院完成课程后，为了弥补上一篇文章中单因素难以量化评估而构建的模型。

笔者构建了一个简单的模型，结合了玩家游戏体验和资源因素去分析moba游戏中，单因素的影响力，即玩家的期望胜率。

模型构造有很多不足，仅停留在一个思路到尝试实践的阶段，虚心接受各位老师的建议和指教，十分感谢！

这是系列文章的第二期，第一期传送门https://gameinstitute.qq.com/community/detail/132720

导读

本篇约7000字阅读需要40分钟，内容有：

l  量化分析的意义：量化的目的的介绍

l  量化分析的思路：量化应该按照的思路

l  截点的选取：选取截点的方法

l  名词解释：重新梳理专用名词

l  模型假设：模型构建的理论前提

l  模型函数：具体的函数表达式

l  模型检验：利用实际的案例分析具体单因素

l  总结

EEA是探娱互动研究院（Explore Entertainment Academy），我们会定期分享我们对游戏研究的文章，希望通过解决一个又一个的命题帮助大家以及我们自己将游戏设计的理论系统化，最终提高生产力。

正文

在moba游戏中，判断事件X（这里的X是可检测到时间点的任意事件）对玩家游戏体验和胜率的影响十分困难，例如丢一龙，拿一龙，送一血，丢一塔，拿一塔，第一次团灭等，在X的发生时刻玩家的感受（对获胜的期望，即主观胜率）无法统计和量化。笔者思考后，构建了一种简单模型，结合玩家体验的角度而不仅是胜率的角度，结合资源因素等，尝试去量化单因素（即事件X）发生时玩家的主观胜率（主观胜率：即结合游戏体验，算出X事件发生时，从玩家主观的角度得出的期望胜率）

量化分析的意义

事件X存在两个状态（例如拿一血和丢一血，拿一塔和丢一塔），对于优势方和劣势方的体验各不相同，这里分析劣势方的角度（即X统一为负面事件），对于优势方分析同理可得。

对于X最直观的评估就是胜率的统计，如果发生X方的胜率约为50％（不可能超过50%，因为X这里是负面事件），那么我们可以得出X事件没有任何影响（负性事件没有任何影响也是不合理的），而如果发生X方胜率约为0％，那么可以认为这件事为非常重要（例如在游戏后期敌方三路兵线上高地时团灭我方）。

但是这里仅仅考虑了胜率的因素，而且只是事后大数据统计上的胜率因素，并不能去计算发生时刻对玩家体验造成的影响，无论失败的玩家是险败还是被碾压，在胜率的数据面前是一模一样，没有任何差异性的，况且这种计算方法并不包括资源因素和时间因素。

从时间的角度看，将X视为第一次团灭，开局的第一次团灭和后期的第一次团灭重要性理应不同（游戏后期团灭导致几乎失败是可以接受的，而前期的团灭如果等同于必然失败是不合理的）应该根据时间的不同赋予不同的权重。

从资源的角度看，被拿一塔或者一血，除了经济差距的200金币外可以直观统计，还包括经验值，视野和兵线运营等等隐性因素难以统计，它们往往藏在其他事件当中，例如一塔丢了导致视野丢失导致野区被反，拿一龙了全队经验或者buff等等(虽然在数据上难以统计)，但是资源因素最终将转换为玩家的游戏体验，因此也是必须得考虑的一部分。

因此，应将资源因素及其背后的隐性影响和时间因素一同加入模型进入考虑。

量化分析的思路

一、我们先考虑处理经济因素和它背后的隐性因素（实际上经济和时间因素是一起考虑的，实际上处理方法也正是如此）

资源因素的考虑十分复杂，经济既可以是一个相对量（用经济差/总经济）也可以是一个绝对量，而经验导致的隐性因素更加难以解释。

考虑到这样的情况，笔者将资源因素转换为玩家游戏体验的角度来分析，根据OPF模型和寂寞模型（参见困局篇），当玩家没有参与合理频率的子闭环的时候，游戏体验将极差。例如在碾压局中后期，逆风玩家已经几乎可以放弃操作，在个体的能力水平限制下，他们只能参与一些高频子闭环，而低频自闭环和中频自闭环（这里可以略过，还是困局篇）已经无法参与。无决策带来的不适感和闭环中的负性反馈让他们没有任何游戏体验。

换句简单的话说，当玩家觉得自己回天无力的时候，就进入了游戏的垃圾时间段（缺少中低频决策自闭环），在这时，游戏没有结束，而翻盘的概率非常地小，落后队伍忍受逆风并到游戏结束。概念类似LOL提到的困局（这里需要一个区分，LOL中的困局是特指垃圾时间很长的对局），但是不可置否的是，垃圾时间的确影响玩家游戏体验。

moba游戏中，在同等水平情况下，所有资源问题都是为经济服务，而经济最终导致了游戏体验问题的出现。所以量化的思路从游戏体验出发，而不是传统的经济因素出发，将游戏时间划分为有效时间（玩家参与分布合理的高中低频子闭环）和垃圾时间（仅仅参与中高子闭环），举例来说，假如游戏30分钟，到了后10分钟的时候，玩家已经完全绝望了，那么有效时间是20分钟，垃圾时间是10分钟。

这里垃圾时间和有效时间的界定应该有一个清晰合理的界限，而不是模糊地认证，而经济因素可以非常清晰明确地判别目前的游戏时间属于有效时间段还是垃圾时间段。在下一节笔者将给出划分标准和计算方法。

二、考虑到发生时间的因素

这里的时间因素指的是X发生的时间t，对于同一件事，它发生的时间是非常影响玩家主观胜率的，例如一塔如果5分钟掉，和15分钟掉，是两个感受不同的结果，因此我们应该给以一个权重。

X的时间的距离垃圾时间段越近，权重应该越大，而X距离垃圾时间段越远权重越小。举例来说，团灭一次之后进入了垃圾时间段，那么我们可以认为这次团灭在这个发生的时间截点对玩家非常重要，应予以一个相当大的权重。

需要说明的一点是，X的发生时间t，一定是在E的范围内，因为在垃圾时间G中，玩家已经回头无力，对胜率的期望极低了，X的发生对玩家的影响已经非常低了。例如，极逆风局的后期（垃圾时间），我方不会因为被敌方击杀一人而降低多少胜率的期望（因为已经期望胜率极低了，下限为0），所以所有对单因素X的考察，只计算有效时间内的。
 

三、综合思路

想要去量化评估玩家的主观胜率（实际上就是量化玩家的游戏体验），需要统计胜率V（victory），X事件发生截点t，游戏总时长T，有效时间E（efficient），垃圾时间G（garbage）。而E和G的划分是通过经济等资源因素的截点（截点的确定需要设计者划分）划分，因此根据这四个自变量（T=G+E，游戏总时长为有效和垃圾两部分，因此不算是一个自变量），就可以拟权重赋值。

需要补充的一点是：我们并不知道过程中玩家对X的胜率期望，这是无法统计和预测的（包括玩家自己也难以准确说出），但是这个模型是通过对结果的分析，包括胜率，经济因素，玩家体验等等，去反推当时的玩家的主观胜率。

举例来说，假如游戏全局体验极为糟糕，我们可以预测，X发生的时候，玩家的期望胜率是不高的，如果玩家最后胜利了，那么越碾压的胜利，玩家对X发生时候，越不在乎（期望胜率越高）。

将所有因素转为的时间上的三个变量（用经济因素去充当截点），用t赋予权重，用E和G去评价玩家体验并计算对期望胜率的数值影响，利用结果反推过程的方法，我们可以量化X发生时，玩家当时的期望胜率（主观胜率）

下面进入一个比较重要的环节：E和G的划分究竟是什么，如何用经济的因素去清晰合理地划分游戏体验期呢？

E和G截点的划分

所以的资源因素都服务于经济因素，而所有的经济因素，在同等水平的前提下，都转换为了用户体验，因此，用经济去划分用户体验时间范围段（E和G）是容易理解并合理的。

经济因素可以是个绝对值（胜利方总经济，失败方总经济），也可以是个相对值（失败方总经济/胜利总经济，双方经济差），绝对值衡量的意义并不大，这里采取相对值，双方经济差D（difference）=胜利总经济-失败方总经济。

而在不同时间点，经济差值意义也不同，5分钟时差2000经济和50分钟差2000经济完全不一样。尤其是moba游戏特有的滚雪球机制，当失败方进入垃圾时间的时候，胜利方可以良性循环，不断扩大优势，以至于经济差拉的非常的大。

所以这里需要用到失败方的结束时的总经济去衡量（有两个优点：一失败方恶性循环，他们的经济增长速率有限，二非常方便统计）

于是得出了最后的截点公式：截点C（critical）=双方经济差/失败方总经济。

其中游戏总时间因素包含在了失败方总经济之中，失败方总经济是随游戏时间增加而单调递增的（不考虑多塔那样的死亡经济惩罚），因此用游戏结束时失败方总经济而不是用事件发生时或者截点处的失败方总经济。

如果截点值稳定大于（是从此刻到游戏结束一直大于，计入先领先后被追上或者反超，此刻依旧算E，只有超过并稳定才算G）某个临界值，我们就可以将其为E和G的划分截点。

截点的选取有很大的主观色彩，而不同的局又有不同的情况，因此必须先确定几条基本原理：

截点的下限选取：双方经济差单调递增（可以保持一样，但不能有明显减少）

截点上限的选取：游戏上升速率最快的点（斜率最大的点），斜率速度最快，表明滚雪球速度越快，正在扩大优势，这时难以翻盘。需要强调的一点是，这里由于是截点的上限，因此同样遵守下限选取的规则，上限选定后，经济差只能继续拉大或者持平，不可明显缩小。

双方经济差＞失败方总经济*0.1（人为选定阙值，向下取整，原因后解）后方可选取截点。

我们将上限和下限确定完了以后，将随机统计20局王者星耀段对局，将每局的平均截点值统计出来，最后加总求平均值。

我们用一个实例来分析一下这个方法：

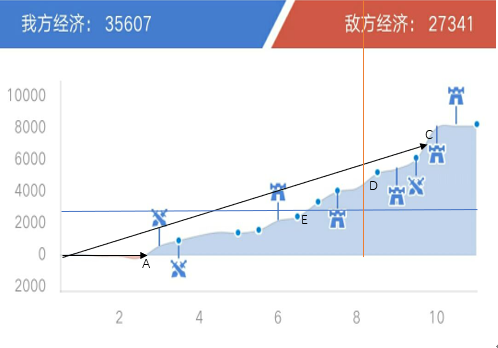
如果我们遵循第一条，则确定了A点，如果我们使用了第二条，则确定了C点，如果如果将截点定在AC之间显然是不科学的，因为A点以后的4分钟内其实优势方经济增长地相当平缓，劣势方完全还有机会将其翻盘，仅属于逆风局。

故我们补充了第三条定理，将阙值的下限赋予了0.1。为什么选取0.1这个点，只是我确定在不超过阙值的条件下，所选取的最大值。我研究了大概30余局对局，截点值从0.12到0.24（这是我个人观看完整局对局以后，人为挑选的截点，用我王者段位的水平观看那局，认为在那个截点以后翻盘率极低，不属于用数据统计的，而是用经验选取的）均有分布，故0.1必然低于实际截点。

为什么不选取0.12作为最低值，因为这个截点总是充满争议，适当缩小阙值，能够减少垃圾时间，增加有效时间，毕竟在垃圾时间的开头部分很多人依然视为有效时间（例如仅仅只有一个人消极游戏，而另外四个队友正积极游戏，对队友来说的消极时间，而对这个消极的人来说，依然属于有效时间）。

故在此图中由于时间上E＞A，故我们选取EC两点作为上下限，取均值。假若A大于E，则我们将选取AC两点作为上下限求均值。也就是说，三条定理共同发挥作用。

这里的E为0.1而C为0.25，求和为0.175，对应找到0.175的截点D点，从直观上来看，是非常符合截点的定义的，同时也符合之前我个人统计出的数据范围。（这里由于统计数据均是星耀2的对局，所以截点仅仅符合星耀2段位左右的对局情况）

构建模型前，将本文出现的名词重新梳理一遍，也同时给以正式的定义和讲解。

模型名词解释

实际上大部分名词在前面已经说过了，但是为了一目了然，再次整理明确一次：

事件X:需要评估的单因素，统一设为负面事件，例如一次团灭、高地被破、超神玩家被击杀（赏金）如需要计算它的正面状态，将最后结果用1减去即可。

发生时间t:从游戏开始到事件X的发生总时间，既可以理解为时间段，也可以理解为时间点。例如一血丢失发生在5分30秒，那么t就等于5分30秒。（因为游戏开始都是从0秒计时）

有效时间E（Efficient）：玩家参与着合理决策频率的子闭环的过程（这个定义在我另外一篇困局分析中有详细介绍）。即在这段时间内玩家对胜负不够明确，在这段时间内仍然积极尝试到达各种目标从而获得胜利的时间过程。

垃圾时间G（Garbage）：对于失败方玩家而言的，玩家参与着分布十分不合理的决策频率的子闭环的过程。即在这段时间内失败方玩家几乎没有希望翻盘，这时无论是否以消极还是积极的态度来对待游戏，对于游戏的失败已经难以挽回。例如在碾压局游戏后期，大多玩家会选择泉水挂机，无论个体玩家做什么都难以阻挡失败，此段时间内玩家游戏体验极差。

碾压时间R（Rolling）：对于胜利方玩家而言的，玩家参与着分布十分不合理的决策频率的子闭环的过程。即在这段时间内玩家已经碾压了对方，只要玩家不采取极端措施（五人一起泉水挂机），在正常情况下，对面难以翻盘的时间段。需要强调的是，对于胜利方来说，这段时间的游戏体验也未必多好，极其容易厌烦（例如高水平玩家打人机，在游戏的中后期几乎没有游戏乐趣）

游戏总时长T：游戏结束的总时间

胜率V（victory）：事件X发生的一方（这里的X被设立为负面事件），实际上的胜率，也就是官方最后统计得出的数值结果，不涉及到任何玩家主观上和过程中的游戏体验。用胜率V可以玩家总数乘以V划分为两个部分：胜利方和失败方，将分别计算他们的期望体验，最后加权求和。

需要说明的一点就是，在同一局中，垃圾时间G=碾压时间R，这很好理解，同一局对决（必须得强调同一局对决中，胜利方和失败方才是相等的。不同局中，E和G分别都有可能不同）中，胜利方进入碾压的时候就是失败方已经游戏体验很糟糕的同一时刻。

而对于同一局，T=E+G（相对失败方）=E+R（相对获胜方）

经过这一系列的准备后，终于可以正式地入手模型的构建，首先从模型假设开始。

模型假设

理性人：玩家都是理性人，他们对自己的判断应该有合理的区间。因为使用的数据很大程度都是赛后数据，是用结果推导过程的。假如游戏中垃圾时间G＞＞有效时间E（极为逆风的对局），玩家在X发生时认为自己胜率是100％，就是极为不合理的，不符合理性人假设。

理性分析（理性人的另外一层面）：玩家对局中有效时间越多E＞＞G，越能客观合理地看待X的胜率。举例，例如官方统计一血丢失方胜率为45％，如果玩家极为逆风（G＞＞E），玩家对此事的评估会低于45%，而如果玩家不但没有失败反而碾压了对方，玩家会对此事的评估高于45%。而玩家如果能积极有效参与整句游戏（E＞＞G），那么他们对X的评估将会越来越准确（趋近于官方统计的实际胜率）

胜率上下限假设：发生X事件的玩家分为两类：，假如官方发生X方的胜率为0.4，那么一类人A发生了并失败了，一类人B发生了并胜利了（这里再次强调X是负面事件，因此人数上，A＞B，即0.6大于0.4）。对于A类人，他们当时的期望胜率是0到0.4，并游戏越逆风越接近0（根据理性分析假设）；对于B类人，他们当时的期望是0.4到1，并且越快碾压对面越接近1（实际上算是理性分析的推论）

后悔规避不计：人对损失的看中是大于收益的，在收益面前人是风险厌恶者，而在损失面前是风险爱好者。（举例：有一半几率获得2000，百分百获得1000，人们会选择1000，而一半几率损失2000，百分百损失1000，人们会选择2000）。这是一个心理学上的问题，这解释了许多坏事为什么主观会比实际要更严重。不过在这个模型中，不考虑心理因素的影响（心理因素因人而异，且很难量化评估。）

实际上，模型假设的就是不考虑心理因素和个体差异（不考虑特别自负和自卑的玩家的极端情况），玩家都是理性的，能大概预测游戏后来的结果，这样根据结果推导的过程才是准确的。（这里不考虑心理因素应该是模型最大的最大的缺陷，如果要完善的话，应该将结果乘以一个权数予以放缩，权数为玩家群体实际心理统计值，这样将结果处理会更符合现实，但是这里仅讨论理论模型。）

模型函数

我们将玩家分为P1和P2两大类，分别是发生了X失败的玩家，和仍然胜利的玩家。

根据模型假设中的理性分析，玩家有效时间E越多越多能精准预测胜率，而垃圾时间G和碾压时间R越长越会影响人的判断。

结合理性人假设，在创建函数时，确立了如下区间

P1的期望胜率P1（E,V,G）∈[0,V];P2的期望胜率P2（E，V，G）∈[V,1]

对于失败玩家P1而言有极端情况两种：

1、发生此事件后直接进入垃圾时间G,说明这件事非常重要，此事发生后期望胜率降低到下限0

2、发生此事后一直是有效时间E，理性的玩家可以对这件事做出客观的评判，期望胜率为V

上下限和时间点确定完以后，两点连线，建立线性相关的函数表达式。

P1（E、V、G）=V-V*G/（T-t）

当G→T-t时，P1（E、V、G）=0

当G→0时，P1（E、V、G）=V

对于胜利玩家P2而言极端情况也有两种：

1、发生此事后直接进入碾压时间R（当然这是不可能的，因为X为负性事件，最多只能趋于），那么说明玩家的实力非常强，他预期的胜率为1

2、此事发生后一直是有效时间E，理性的玩家可以对这件事做出客观的评判，期望胜率为V

上下限和时间点确定完以后，两点连线，建立线性相关的函数表达式。

P2(E、V、G)=V+（1-V）*R/(T-t)

当R→0时，P2（E、V、G）=V

当R→T-t时，P2（E、V、G）=1

最后将两者加权求和，得出我们的总期望胜率P

P=（1-V）*P1+V*P2

= （1-V）（V-V*G/（T-t））+ V^2+（1-V）*V*R/(T-t)

=1-(1-V)*V*(G-R)/(T-t)

模型检验

目前选取星耀2对局中，随机选取10局游戏（选取方法，随机点击对面的对手查看最新的一局排位对局后再从他的对局中选取一位他的对手。）人力有限，故统计局数无法太多，可能会有一些计算偏差，见谅。

​

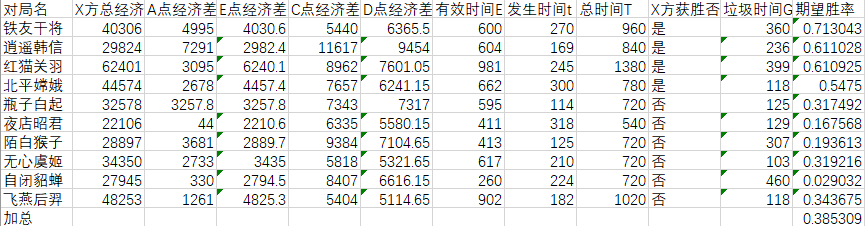
如图，设丢失一塔为X事件，随机统计10局后，最后计算出的期望胜率是百分38.5，低于统计值的百分之40，这里的38.5是对玩家主观感受的一种侧面计算，而非是统计上的数字，模型检验得出的结果表明，丢一塔对玩家造成的影响，比实际上的结果值要稍微高一些（实际上无论是从关联记忆还是从心理学上来说，人们更加看重损失而非收益）

不过介于统计数据过少的原因，精准程度仍然有待加强。

这不仅仅只能评价负面事件，包括正面事件是一样可以评价，只要将胜率统计出来，玩家分类后计算出不同玩家的期望胜率，最后加总求和即可。

总结

判断一个事件或者是背后的一个机制（例如赏金，一血机制等）究竟是否合理首先自然是看它发生后的胜率是否符合设计者的期望，但是玩家体验不仅仅只是最后胜率所能完全表现出来，要想探寻玩家的真实感受，需要结合游戏过程中的游戏体验，资源分布，时间截点等等。

可以举个例子帮助理解，假如有100局对局发现了X事件，其中45局X方玩家获得了胜利，65局玩家输了对局。然而45％的胜率仅仅只能一定程度上反映是否合理，但是它无法衡量那65局玩家的游戏体验，无论是险败还是被吊打碾压，在数据上均只是衡量为45％，而上述方法通过玩家的游戏体验，将游戏分为两个阶段，来计算玩家的体验，最后加权求值，反映一个更加接近玩家体验的胜率。

这仅仅是一个初步的设想，实际上可以完善的地方还有很多，例如甚至可以将游戏时间分为三个部分，而B截点确定的方法需要根据游戏本身和经验，具体问题具体分析，是一个需要根据不同游戏甚至不同段位调整的一个阙点，背后的方法并没有完善和格式化。

本文通过建立模型，希望提供一种思路，在考虑一个机制在游戏中是否合理的时候，可以添加玩家感受进入模型，得到更为真实的量化数据和统计胜率结合，一起衡量这个游戏机制问题。