Voronoi Diagram（维诺图）

很久没写点东西了了，整理一些之前的一些知识点。大部分还是些图形处理方面的，现从简单的开始：

Voronoi Diagram（维诺图） ，文章最后会附上自己撸的源码连接。

看到这个算法时，突然想起了我们当年做的《指上谈兵》这款手游里面地图的处理。在这Voronoi图划分好的大致范围内再稍微处理一下，完全可以胜任我们当时对地图势力范围切换方面的处理效果。

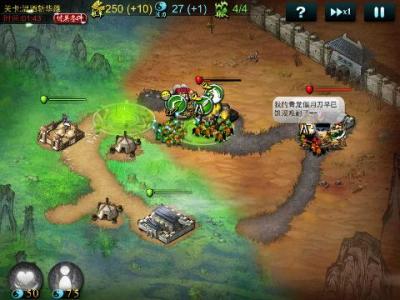
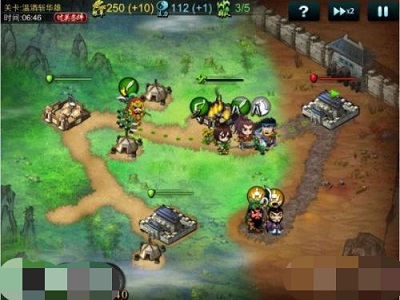
如上两图所示，地图中每个城池都有自己的势力范围，在城池被我方攻陷后，背景地图会产生颜色的变化。这个是在shader中对两张图进行混合来做的。而每个城池的势力范围用Voronoi Diagram应该有不错的表现效果。

Voronoi Diagram

又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。N个在平面上有区别的点，按照最邻近原则划分平面；每个点与它的最近邻区域相关联。Delaunay三角形是由与相邻Voronoi多边形共享一条边的相关点连接而成的三角形。Delaunay三角形的外接圆圆心是与三角形相关的Voronoi多边形的一个顶点。 Delaunay三角形是Voronoi图的偶图；

根据点集划分的区域到点的距离最近，其在众多领域具有广泛的应用。如在障碍物点集中，规避障碍寻找最佳路径。

Delaunay

点集的三角剖分（Triangulation），对数值分析（比如有限元分析）以及图形学来说，都是极为重要的一项预处理技术。Delaunay三角剖分有最大化最小角，“最接近于规则化的“的三角网和唯一性（任意四点不能共圆）两个特点。

算法分析

先Delaunay算法对所有离散点构网，找出三角网中每个三角形的外心（外接圆圆心），最后连接相邻三角形的外心（边界三角形需要计算射线交点），形成以三角形顶点为元的多边形网。

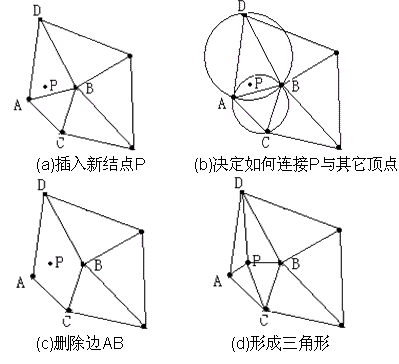
• Delaunay算法的基本步骤是（实现算法有很多种，感兴趣的可以自行搜索）： 

1. 构造一个四边形边框，包含所有散点，放入三角形数值中。 
2. 依次插入散列点，判定是否在之前三角形外接圆内，若在内，则提取其边为检测边界，并删除该三角形。
3. 将提取的边界与新插入的散列点组成新三角形。
4. 循环执行上述第2步，直到所有散列点插入完毕。

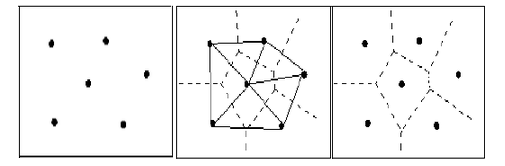
• 建立Voronoi图的步骤为：

1. 将Delaunay构建的结构进行分析整理，将三角形的每条边与其邻接三角形、每个顶点与其关联的边都建立管理。
2. 遍历三角形顶点，然后遍历该顶点所管理的所有边
3. 若该边关联两个三角形，则将两三角形的外心连接形成图元多边形的一个变。
4. 若该边只关联一个三角形（边界三角形），则将三角形的外心为起点，边的向外垂线方向为射线方向，做一条射线，与最外边框形成封闭边。
5. 遍历结束，所有维诺边被找到，根据边画出维诺图。 
   
    

具体代码就不在这贴了，感兴趣的同学可以访问下面的连接，代码都放在git上了

算法用C++实现，显示用OpenCV来处理的（以实现功能为主，没怎么优化整理）

https://github.com/ArtStealer/Voronoi_Delaunay

也欢迎关注我的公众号，我会时不时的分享一些技术干货，欢迎关注互动讨论：