图形硬件上基于图块的纹理映射

截取主要章节进行翻译。完整论文请参照http://graphics.stanford.edu/papers/tile_mapping_gh2004/

 3.总览 
 我们的目标是设计一种结合了先前方法优点的新算法。 该算法应足够通用，以处理具有重复图案的纹理。 对于图形硬件实现，它应该简单，高效并且消耗最少的纹理内存。 它应该支持纹理过滤和mipmapping。 它也应该对应用程序无干扰，并且不需要修改输入几何或纹理坐标。 

 我们试图通过使用Wang Tiles [CSHD03]直接在GPU上生成大型虚拟纹理来实现这些目标。 Wang瓷砖是正方形瓷砖，在其中为每个瓷砖边缘分配了一种颜色。 有效的平铺要求平铺之间的所有共享边都具有匹配的颜色。 当一组Wang瓦片中填充有在匹配的瓦片边缘上连续的纹理图案时，来自该组的有效拼贴可以产生任意大的纹理而不会出现图案间断。 [CSHD03]讨论了从样本图像构造此类图块集的技术，并提出了用于非周期性图块的顺序算法。 

 我们提出了一种基于Wang Tiles的新纹理映射算法。 我们的算法动态地组合了这些图块，以构建大型的虚拟纹理而不是物理存储。 作为预处理步骤，我们将这些图块打包为单个纹理贴图，并且当从此图块包中提取纹理像素时，我们的打包方案可确保正确的mipmap过滤。 在运行时，对于每个纹理请求（s，t），我们首先根据（s，t）在输出纹理内的位置确定其到达的输入图块。 然后，我们计算该输入图块中（s，t）的相对偏移，并从输入包中获取相应的纹理像素。 由于输出打包方案支持正确的Mipmap过滤，因此获取的输入纹理像素将看起来与从大型的，物理存储的纹理图中获取的纹理像素相同。 我们的系统概述如图1所示。 

 我们的贡献如下。 我们提出一种新的切片技术，以允许在任意切片上进行随机访问。 我们提出了一种将这些图块打包到纹理内存中以支持mipmap过滤的新方法，并演示了我们的算法在图形硬件上的有效实现。 

 4. 基于图块的纹理映射 

 纹理映射的目标是为每个具有纹理坐标（s，t）的屏幕像素分配纹素 Tex（s，t）。 当前的图形硬件将整个纹理存储在内存层次结构中，并通过获取和过滤相关纹理像素来实现Tex（s，t）。 这种方法对于可以放入片上纹理缓存或片外纹理内存的小纹理效果很好，但是难以存储和访问无法放入可用纹理内存的大纹理。 

 我们为Tex（s，t）提供了一种替代方法，TileTex（s，t），该方法不需要大量纹理存储。 TileTex（s，t）提供与传统Tex（s，t）相同的接口，支持对大纹理进行过滤和mipmapping。 在内部，TileTex（s，t）使用一小部分Wang Tiles代表一个大纹理，并即时将这些瓦片组装成一个大的虚拟纹理，以响应纹理请求。 请注意，我们的算法完全在纹理空间上实现，不需要应用程序修改输入几何或纹理坐标。 现在我们描述基于图块的纹理映射算法TileTex（s，t）。 

 4.1 输入样本的纹理平铺构造 

 我们算法的输入包括样本纹理S，单个图块大小Th Tv，南（S）和北（N）边缘的水平颜色Kh数量，以及东（E）和 西（W）边缘的垂直颜色Kv数量。 这些输入参数的含义与[CSHD03]中的含义相同，我们直接采用它们的方法来构建Wang Tile集。 

 但是，[CSHD03]与我们的方法之间在所需的图块数量上仍存在重要区别。 [CSHD03]使用顺序切片方法，仅需要Kh x Kv x 2切片即可支持所有可能的NW颜色组合用于非定期切片。 由于我们的方法支持非顺序的随机图块访问，因此我们要求Kh^2 x Kv^2图块支持所有可能的边缘颜色组合。 与[CSHD03]相比，这是我们方法的缺点。 但是，我们尚未发现这是一个主要问题，因为实际上Kh和Kv通常都很小（对于非周期性平铺来说，2就足够了）。 此外，具有完整颜色组合的图块集还具有其他优势，例如易于支持连续包装以进行纹理过滤，这将在后面介绍。 

 4.2。 用于随机访问的纹理图块映射 

 构建图块集后，我们可以对其进行平铺以生成任意大的纹理。 为了确保连续的纹理图案，需要进行平铺，以便所有共享的图块边缘都具有相同的颜色。 一种实现这种平铺的方法是，将瓷砖从北向南，从西向东依次放置，如[CSHD03]所示。 但是，顺序切片有一个轻微的缺点，即如果仅访问SE切片，我们仍然需要计算整个切片，以确保最终在SE角获得相同的切片配置。 这可能会导致图形硬件实现的效率问题。 

 一种可能的解决方案是预计算图块映射并将结果存储在索引纹理图中。 但是，对于由小图块组成的大型输出纹理，索引纹理仍然可能太大。 

 我们的方法是即时计算图块映射，而不是存储预先计算的索引图。 为了实现渲染一致性，我们要求映射计算必须是可随机访问的，这意味着每个图块的计算可以独立执行，同时确保所有共享图块的边缘具有相同的颜色。 这避免了顺序依赖性问题，并导致更快的计算。 我们的图块映射计算TileMap（s，t）如下： 

 (1)对于输入纹理坐标(s,t)，计算其所位于的输出图块。假设输出纹理包括Mh个水平块和Mv个垂直块。然后可以通过以下方式计算输出的图块索引(Oh, Ov): 
 （Oh, Ov） = floor((s, t) * (Mh, Mv)) % (Mh, Mv)  (1) 
 其中％是取模运算符。 我们将％用于环形边界处理，但可以很容易地将其扩展为其他边界环绕模式。 

 (2)使用(Oh, Ov)来随机输出块的四个边的颜色值CS,CE,CN,CW，如下所示: 

 Cs = hash[hash[Oh] + Ov] % Kh 
 Ce = hash[(Oh + 1) % Mh + hash[2 * Ov]] % Kv 
 Cn = hash[hash[Oh] + (Ov + 1) % Mv] % Kh 
 Cw = hash[Oh + hash[2 * Ov]] % Kv 

 其中hash []是一维哈希函数，目前我们通过[Per02]中所述的置换表来实现。 我们发现使用具有max（Mh，Mv）项的hash []表就足够了。 由于Mh和Mv通常很小，因此hash []的缓存和存储通常不是问题。 
 

 图3：哈希表大小对公式2的影响。图像大小为32 32，每个像素颜色编码为CS，CE，CN和CW的唯一组合 

 我们的映射计算受到名为“猫图” [XGS00]的离散混沌图的启发。 在Cat-Map中，一对整数（x,y）通过以下方式映射到新位置（x0,y0） 

 x0 = x + y 
 y0 = x + 2*y 

 Cat-Map有助于打破对角线对称性并增加瓷砖贴图计算中的随机性。 在上述等式中，直接从Cat-Map中采用CS和CW，而从CS和CW派生CN和CE以保持边缘颜色的一致性。 例如，考虑图块（Oh，Ov）及其E侧的图块（Oh + 1，Ov）。 上面的计算可确保（Oh，Ov）的CE与（Oh + 1，Ov）的CW相同。 类似的论点可以应用于CS和CN的计算。 

 选择具有相应4种边缘颜色的输入图块。 由于我们的图块集具有完整的颜色组合，因此这始终是可能的。 
 总而言之，给定纹理坐标（s，t）的纹素请求，上述步骤将计算TileMap（s，t），指定要落在哪个输入图块（s，t）上。 输入图块由边缘颜色CS，CE，CN和CW指定。 

 4.3 纹理图块访问和过滤 

 在知道纹理请求（s，t）位于哪个输入图块I（CS,CE,CN,CW）之后，我们需要找出图块内（s，t）的相对位置以获取正确的纹理像素。 相对位置（δh，δv）可以通过下列计算得出: 
  (δh，δv) = fraction((s,t) * (Mh, Mv))   (4) 
 其中fraction（）取浮点值的小数部分。 对于最近邻纹理采样，最终纹理元素值TileTex（s，t）将来自相应输入图块中最接近的纹理元素（δh，δv）。 对于其他采样模式，例如双线性或各向异性过滤，问题将更加复杂。 如果（δh，δv）距图块边界足够远，则足以在该图块内执行所需的滤波操作。 但是，如果（δh，δv）靠近边界，则正确的滤波将涉及输出纹理中相邻图块的纹理像素。 由于输出纹理是虚拟的，因此无法在图形硬件上直接执行此过滤操作。 

 当（δh，δv）接近边界时，有几种支持滤波的方法。 一种可能的解决方案是将纹理过滤模式设置为点采样，并使用片段着色器执行纹理过滤。 这是最灵活的方法，因为我们可以跨图块边界访问任何纹理元素，但是由于我们需要请求许多纹理样本（三线性mipmap过滤需要8个样本，而各向异性过滤可能需要更多），因此它可能很慢。 通常，让纹理单元执行纹理过滤更为有效，因为与片段着色器内部的算术运算相比，纹理读取相对较慢。 

 但是，由于在存储的纹理图中执行了硬件纹理过滤，因此我们必须找到一种方法来存储Wang Tiles集以支持正确的过滤。 有几种可能的方式来存储图块。 一种解决方案是将每个图块存储为单独的纹理。 由于大多数硬件的可绑定纹理数量有限，因此我们可以快速用完纹理ID。 这种方法也不能正确处理图块边界条件。 另一种解决方案是将所有图块打包到一个纹理贴图中。 假设输入的图集具有Ph个水平图块和Pv个垂直图块，并且所需的输入图块位于此图集中的第（Ih，Iv）个图块中，那么我们可以获取偏移量（δh， δv）如下：  
   TileTex(s,t) = Tex((Ih+δh)/Ph, (Iv+δv)/Pv)     (5) 
 该方案的挑战是确保跨输出图块边界的纹理过滤可以作为输入图块包中的过滤执行。 为了实现此目标，我们提出了一种利用现有硬件纹理过滤和mipmapping功能的打包方案，并描述了如何在这种打包方案中从图块边缘颜色（CS，CE，CN，CW）有效地计算（Ih，Iv）。 

 4.4 纹理块打包和角的处理 
 将纹理图块打包到一个纹理图中，我们希望实现三个目标。 首先，为了利用最少的纹理内存，每个图块在打包的纹理中应该只出现一次。 其次，为避免过滤纹理块边界上的伪像，打包纹理中的相邻块应具有匹配的边缘颜色。 第三，打包方案应支持有效的索引编制。 也就是说，给定输入图块I（CS; CE; CN; CW）的边缘颜色描述，打包方案应有效地计算I（CS,CE,CN,CW）的水平和垂直索引（Ih，Iv） 内包装的纹理。 

 我们提出了一种新的图块打包方案TilePack，它试图满足上述要求。 为了澄清起见，我们首先描述如何以1D方式打包图块。 然后，我们描述如何将其扩展到2D。 

 假设我们有一组Wang Tile，它们具有Kv种垂直边缘颜色，但只有一种水平边缘颜色。 我们的目标是将这些图块打包在水平行中，以使相邻图块具有匹配的垂直边缘颜色（包括最左边和最右边的图块，因为打包的纹理需要可平铺）。 我们将所有垂直边缘颜色编码为[0..Kv-1]范围内的整数。 给定一个具有西边和东边颜色（e1，e2）的图块，我们使用以下映射来确定该图块在打包的1D纹理内的水平位置：（推导此公式的过程可以在附录A中找到。) 
 

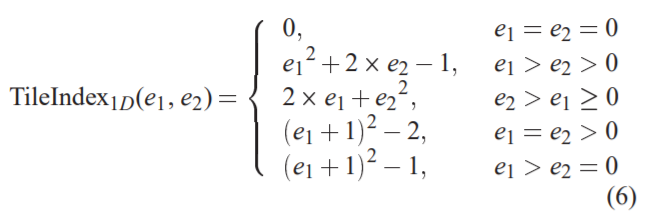
  TileIndex1D(e1, e2) =  
   0,      e1=e2=0 
   e1^2 + 2*e2-1,  e1>e2>0 
   2*e1+e2*e2,   e2>e1>=0 
   (e1+1)*(e1+1) - 2, e1=e2>0 
   (e1+1)*(e1+1) - 1, e1>e2=0        (6) 

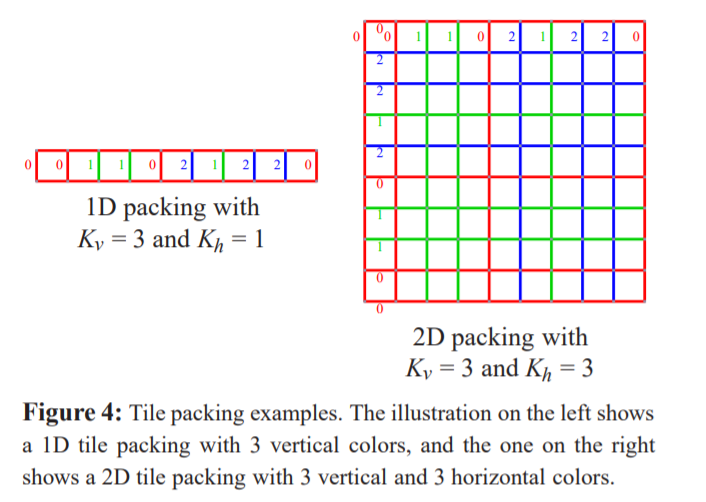
 TileIndex1D满足上面列出的三个要求。 它将Kv*Kv图块打包为水平1D纹理贴图，而不会多次使用任何图块。 这样可以确保所有共享的图块边缘具有相同的颜色。 此外，它仅包含乘法，加法和减法即可高效地进行计算。 图4显示了Kv = 3的一维打包的示例. 

 如公式7所示，我们可以在水平和垂直颜色上通过TileIndex1D正交实现2D TileIndex。给定具有边缘颜色（CS，CE，CN，CW）的图块，图块的水平索引Ih由TileIndex1D（CW， CE），而图块的垂直索引Iv由TileIndex1D（CS，CN）计算。 由于TileIndex1D满足1D中的三个要求，并且（Ih，Iv）是正交计算的，因此可以很容易地看出TileIndex1D满足2D中的三个要求。 Kh = 3和Kv = 3的2D打包示例如图4所示。 

  (Ih, Iv) = TileIndex(CS, CE, CN, CW ) = (TileIndex1D(CW, CE), TileIndex1D(CS, CN)) (7) 

 我们的图块打包方案的主要优点之一是，它允许我们直接通过硬件纹理处理单元执行纹理过滤。 由于包装中的相邻图块共享匹配的边缘颜色，因此在跨图块边缘执行双线性过滤时不会出现图案不连续性。 但是，双线性滤波在整个图块角上在理论上可能是不正确的。 解决此问题的一种方法是简单地忽略它。 我们已经发现，只有在瓷砖角附近放置了与众不同的物体或图案时，此角人工痕迹才可见。 对于具有统一重复图案的纹理，这通常不是问题。 

 另一种解决方案是添加具有所有可能的边角组合的附加图块图集。 该解决方案将允许在图块角上进行正确的过滤，但会消耗额外的纹理内存和着色器计算量。 此角部填充的派生与上面的图块填充类似，有关更多详细信息，请参阅附录B。 

整个完整的流程: 
输入： 
S：采样的贴图 
Th * Tv : 单个图块的像素分辨率 
Kh, Kv : 水平和垂直边的颜色数量 
Mh*Mv : 输出图片的大小是由多少块单个图块组成的 

预处理: 

从贴图S构建Wang Tiles 
将图块打包到TilePack中 
(Ph, Pv) = (Kv*Kv, Kh*Kh) 

运行时: 
(Oh, Ov)= floor((s,t)*(Mh, Mv))%(Mh, Mv)  图块坐标 

(Cs, Ce, Cn, Cw) = EdgeHash(Oh, Ov)  等式2 

(Ih, Iv) = TileIndex(Cs, Ce, Cn, Cw)  等式7  图集索引 

(δh, δv) = fraction((s,t) * (Mh, Mv)) 

ue = Tex((Ih + δh)/Ph, (Iv+δv)/Pv) //从TilePack取像素