我说我为什么抽不到SSR,原来是这段代码在作祟
【本文参与GWB更文挑战活动-首发原创】,联系方式(微信):ggw1315
本文所有代码使用 Go 语言实现。
因为编辑器不支持代码块,所以提高可读性,选择使用图片预览代码、数学公式等,本文所有代码都在文末的地址中。
灵魂拷问
为什么有 50% 的几率获得金币?
为什么有 40% 的几率获得钻石?
为什么只有 9% 的几率获得装备?
为什么才有 1% 的几率获得极品装备?
什么是加权随机?当我们从某种容器中随机选择一个元素,每个元素被选中的机会并不相等,而是由相对“权重”(或概率)被选中的,也就是说我们想要有“偏心”的得到某种随机结果。举一个例子,假如现在有一个权重数组 w = { 1, 2, 4, 8 },它们代表如下规则。

解决方案
方案一、笨笨的办法
第一个方法是在我们的候选列表中,包含了基于权重的每个索引的预期数量,然后从该列表中随机选择。
假设现在有权重列表 { 1, 2, 4, 8 },那我们得到的候选列表将是 { 0, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3 }。
然后通过 rand.Intn() ,获取一个随机数,就完成了,代码如下。

方案二、略显聪明
使用方案一,当权重特别大的时候,这种方案显然效率不高,会浪费很多时间来生成列表,并占用太多的内存。
方案一中的列表不是必须的,方案二避免生成大的列表。由于总权重为 15(1+2+4+8),我们可以生成一个 [0,15) 的随机整数,然后根据这个数字返回索引。代码如下。

方案三、神之一手
方案二避免了方案一中的生成列表,因此效率更高了。但是我们必须写很多的 if else 代码,这看起来太难看了,为了避免编写过多的 if else 代码,衍生出了方案三。
不必将 r 与所有的范围进行比较。我们可以依次减去总权重,任何时候结果小于等于零,我们就可以返回它。这种方法可以叫做放弃临时名单。

方案四、小小优化
对于方案三,r 小于等于 0 的速度越快,我们的算法就越高效。那么我们如何让 r 到达 0 更快呢?
直观感受上,如果 r 减去最大的权重,就会更快到达 0 ,所以在运行 weightedRandom 前,我们可以对 weights 按照权重从大到小排序。

可以通过数学期望来证明我们的想法。
最佳顺序
{ 8, 4, 2, 1 }
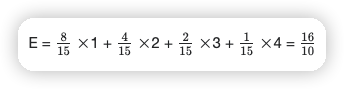
相对最佳顺序,较差的顺序
{ 2, 4, 8, 1 }
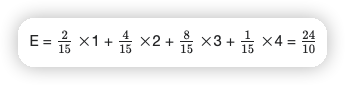
最差的顺序
{ 1, 2, 4, 8 }
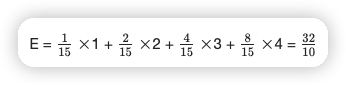
可以看到,最佳顺序,即权重从大到小的排序。
方案五、不可思议
方案四中,实际上引入了一个新的耗时步骤,我们必须对 weightedRandom 排序,当这是一个很大的列表时,效率也就被拉低了。
在方案五中,我们考虑使用累积权重,而不是原始权重。并且由于累积权重是升序排序的,我们可以使用二分来加快速度,因为二分查找可以将时间复杂度从 O(n) 变为 O(log(n))。

方案六、不死不休
到目前位置,我们的解决方案已经足够好了,但是仍然有改进的余地。
方案五中,我们使用了 go 标准库的二分查找算法 sort.SearchInts() ,它这是封装了通用的 sort.Search() 函数,如下。
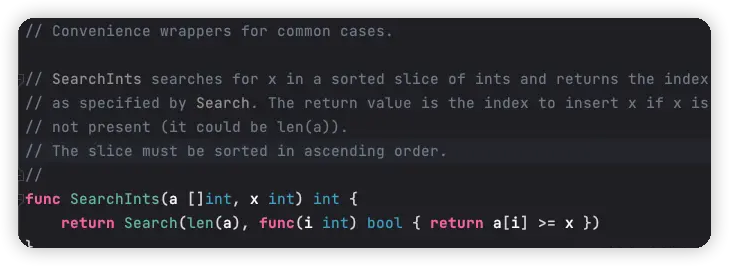
sort.Search() 的函数参数需要一个闭包函数,并且这个闭包函数是在 for 循环中使用的,如下。
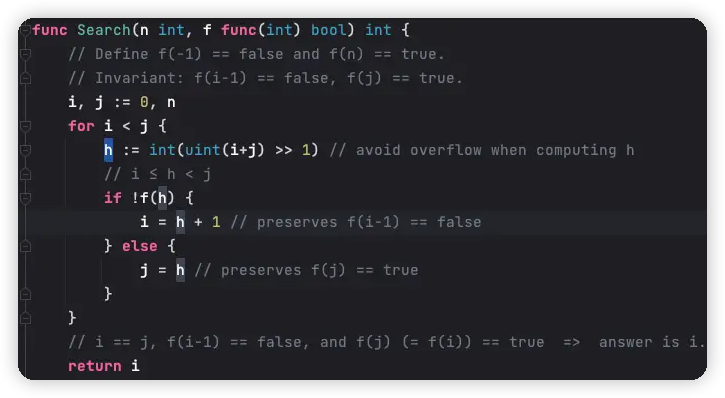
所以目前无法被编译器正确地内联,从而导致了非实质性的性能开销,在方案六中,我们可以编写一个手动内联的版本。

通过基准测试可以看到吞吐量提升了 33% 以上。对于大型数据集,优势越明显。
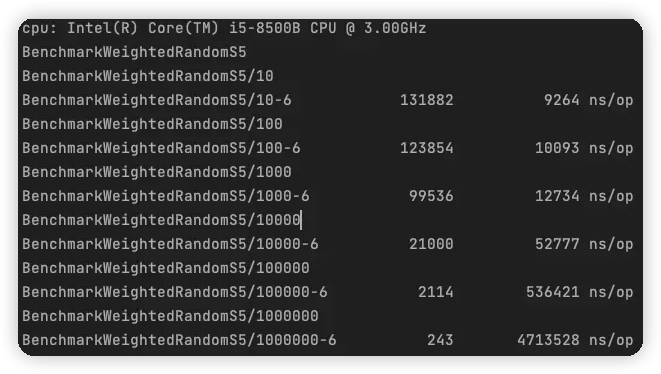
优化前
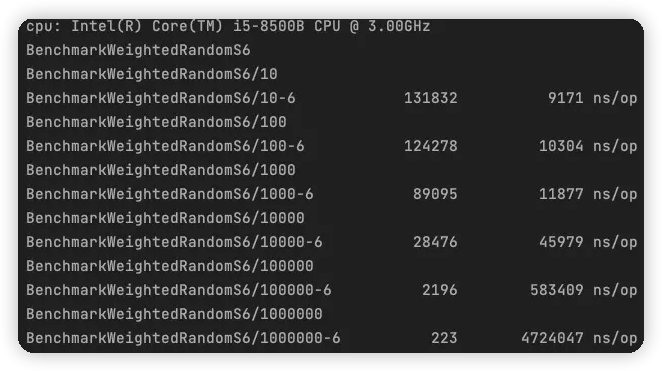
优化后
方案七、轮盘赌
目前为止我们所有的方案都有一个共同点 —— 生成一个介于 0 和权重之和之间的随机数,并找出它属于哪个“切片”。
还有一种不同的方法。

这个算法的一个有趣的特性是你不需要提前知道权重的数量就可以使用它。所以说,它或许可以用于某种流。
尽管这种方案很酷,但它比其他方案慢得多。相对于方案一,它也快了 25% 。
源代码
