SPH算法简介（五）：表面张力的计算

        所谓表面张力，正如前面所讲，就是由于流体“试图减小表面积”而产生的力，这种力产生的效果非常有趣，它会使肥皂膜紧绷，使水滴变成球形，但在大部分SPH应用场合中，和其他力相比，表面张力产生的效果其实是微乎其微的，所以常常忽律表面张力的计算。
        如果要想计算表面张力，就要考虑它的特殊性质，首先只有位于流体表面的粒子才会受到表面张力的影响，所以第一个问题就是如何找到那些处于“表面”的粒子。
        首先构造这么一个标量场，在有流体粒子的位置都染上一个“颜色值”1，其他位置的”颜色值”都是0，针对二维情况说明，这就好像构造了类似于一个“高度图”的标量场。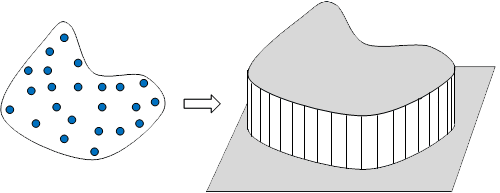

        根据光滑核原理，流体内任意一点r所在位置的“颜色”值为

	(5.1)

        对这个标量场做哈密顿运算，回想一下我们以前提到的梯度的概念，所得到的梯度场∇cs可以给我们两个信息，第一，由于梯度反应的是标量场中“变化的程度”，所以只有在流体的边界部分才会有比较大的梯度值，而内部的梯度值几乎为0，根据这个特性可以用来判断粒子是否处于表面，第二，梯度场的方向指向大值部分，也就是流体的内部，而这正是表面张力的方向。

        而表面张力的大小，则跟流体表面的“曲率”有关，这个值可以根据颜色值的拉普拉辛算子计算

	(5.2)

        最终的表面张力还需要乘上一个系数和方向矢量：

	(5.3)

        其中σ被称为表面张力系数，跟流体的材质有关，所使用的光滑核函数和计算密度时的一样，都是Poly6，在3D情形下，它的哈密顿形式和拉普拉辛形式分别是：

	(5.4)

	(5.5)

        最后可以求出受表面张力影响，粒子产生的加速度部分

	(5.6)