SPH算法简介（三）: 光滑核函数

        和其他流体力学中的数学方法类似，SPH算法同样涉及到“光滑核”的概念，可以这样理解这个概念，粒子的属性都会“扩散”到周围，并且随着距离的增加影响逐渐变小，这种随着距离而衰减的函数被称为“光滑核”函数，最大影响半径为“光滑核半径”。

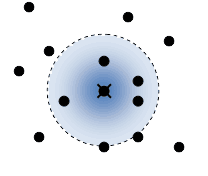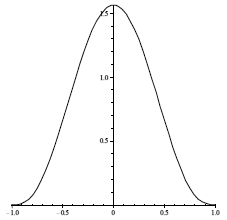	光滑核函数一般具有的形态

        反过来不难理解，尽管我们将流体视为一个个分散的粒子，但流体毕竟是连续充满整个空间的，流体中每个位置参与运算的值都是由周围一组粒子累加起来的。


        设想流体中某点r（此处不一定有粒子）,在光滑核半径h范围内有数个粒子，位置分别是，r0, r1, r2, …, rj，则该处某项属性A的累加公式为：

	(3.1)

        其中Aj是要累加的某种属性，mj和ρj是周围粒子的质量和密度，rj是该粒子的位置，h是光滑核半径。函数W就是光滑核函数，光滑核函数两个重要属性，首先一定是偶函数，也就是W(-r)=W(r)，第二，是“规整函数”，也就是∫W(r) dr=1

	(3.2)

        也就是说，需要逐个推出密度ρ，压力p，速度u相关的累加函数，我们逐个来分析

	(3.3)

密度

        计算使用的光滑核函数称为Poly6函数，具体形式为:

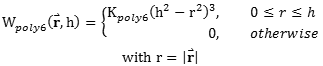	(3.4)

        其中，KPoly6是一个固定的系数，根据光滑核的规整属性，通过积分计算出这个系数的具体值，在2D情况下，在极坐标中计算积分：

	(3.5)

        3D情况下，在球坐标中计算:

	(3.6)

        由于所有粒子的质量相同都是m，所以在3D情况下，ri处的密度计算公式最终为：

	(3.7)

压力

        根据上一节的结论，在位置ri之处的由压力产生的作用力的计算公式为

	(3.8)

        不过不幸的是，这个公式是“不平衡”的，也就是说，位于不同压强区的两个粒子之间的作用力不等，所以计算中一般使用双方粒子压强的算术平均值代替单个粒子的压力

	(3.9)

        对于单个粒子产生的压力p,可以用理想气体状态方程计算

	(3.10)

        其中ρ0是流体的静态密度，K是和流体相关的常数，只跟温度相关。
        压力计算中使用的光滑核函数称为Spiky函数

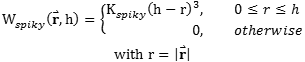	(3.11)

        在3D情况下，KSpiky=15/(π*h^6)

	(3.12)

        现在可以整理出公式3.2中压力产生的加速度部分

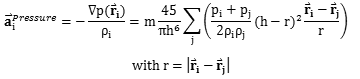	(3.13)

粘度

        现在把注意力集中到公式3.2中最后一部分，由粘度产生的加速度

	(3.14)

        这个公式同样有不平衡的问题，考虑到公式中的速度其实并不是绝对速度，而是粒子间的相对速度，所以这个公式的正确写法应该是：

	(3.15)

        其中的光滑核函数形式如下：

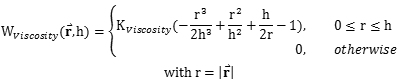	(3.16)

        在3D情况下，KViscosity=15/(2*π*h^3)

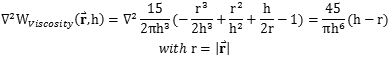	(3.17)

        由此可得到公式3.2的粘度部分

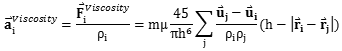	(3.18)

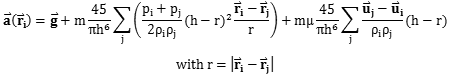	(3.19)

        好了，我们似乎推导出一大推复杂的公式，不用担心，你已经过了最困难的部分，下一节我们来点真的，让这些公式运行起来看看