SPH算法简介（一）: 数学基础

        SPH(Smoothed Particle Hydrodynamics)算法是一种流体模拟算法，他的特点是简单快速，可以用在例如游戏这样的实时的交互软件中。SPH算法虽然简单，但要完全搞明白其中的原理和实现方法，也不是易事，写这个系列希望能全面介绍一下相关的内容，如果你搜索到这里，可以仔细看一下这个系列，希望能帮到你。

        烟雾、海浪、水滴…，这些司空见怪的自然现象其实有着非常复杂的数学规律，对于流体的研究，有两种完全不同的视角，分别是欧拉视角和拉格朗日视角。欧拉视角的坐标系是固定的，如同站在河边观察河水的流动一样，用这种视角分析流体需要建立网格单元，还会涉及到有限元等复杂的工程方法，一般用在离线的应用中。而拉格朗日视角则将流体视为流动的单元，例如将一片羽毛放入风中，那么羽毛的轨迹可以帮我们指示空气的流动规律。

欧拉视角和拉格朗日视角

       SPH算法是典型的拉格朗日视角，它的基本原理就是通过粒子模拟流体的运动规律，然后再转换成网格进行流体渲染。

		>		>

	(1.1)

        例如，定义z=x2+2xy+y3，那么∂z/∂x=2x+2y, ∂z/∂y=2x+3y2

哈密顿算子

        哈密顿算子∇在流体力学中是如此重要，以至于很多地方将这个符号作为流体力学的标志，所以这里要着重介绍一下，所谓“算子”，就是那种不能单独存在，必须和其他符号放在一起的一种数学符号，例如微分中的那个“d”。哈密顿算子的定义如下：

	(1.2)

        哈密顿算子有很多有趣的特性，它本身虽然并不是一个矢量，但很多运算确实可以把它视为一个矢量，例如把它作用在一个标量场A=f(x,y,z)上，那么

	(1.3)

        这个运算可以视为一个矢量和标量的乘法，得到的∇A是一个矢量场，称为A的“梯度”，顾名思义，梯度的含义就是标量场A在某处变化快慢和方向，比如一个标量场H(x,y)是一座高山在(x,y)处的高度，则H的梯度是该高山在某处陡峭的程度，并且方向指向高处。

　　上面两个图中，标量场是黑白的，黑色表示大的数值，而其相应的梯度用蓝色箭头表示

        而如果把哈密顿算子作用在一个矢量场A上，得到的∇∙A称为矢量场A的“散度”，散度的计算和矢量的点积运算相似，得到的是一个标量场。

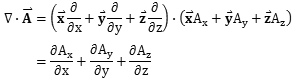	(1.4)

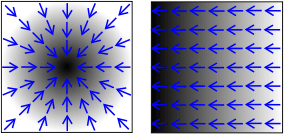
        散度的意义也很明显，就是描述一个矢量场“发散”的程度，例如下面的两个矢量场，左边的有很大的散度，而右边的散度为0

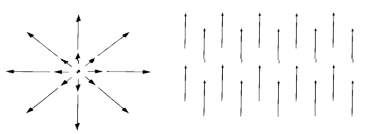
两个散度差别很大的矢量场

拉普拉辛算子

拉普拉辛算子∇2是二阶微分算子，有时也可写作Δ或者∇∙∇

	(1.5)

        例如对于A=f(x,y,z)

	(1.6)